Answer:
A. number of decayed atoms = 73.197
Explanation:
In order to find the answer we need to use the radioactive decay equation:
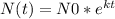 where:
where:
N0=initial radioactive atoms
t=time
k=radioactive decay constant
In our case, when t=0 we have 1,000,000 atoms, so:
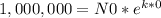
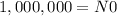
Now we need to find 'k'. Using the provied information that after 365 days we have 973,635 radioactive atoms, we have:
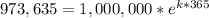
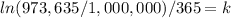
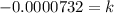
A. atoms decayed in a day:
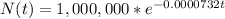
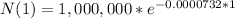
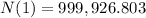
Number of atoms decayed in a day = 1,000,000 - 999,926.803 = 73.197
B. Because 'k' represents the probability of decay, then the probability that on a given day 51 radioactive atoms decayed is k=0.0000732.