Question

When studying radioactive​ material, a nuclear engineer found that over 365​ days, 1,000,000 radioactive atoms decayed to 973 comma 635 radioactive​ atoms, so 26 comma 365 atoms decayed during 365 days. a. Find the mean number of radioactive atoms that decayed in a day. b. Find the probability that on a given​ day, 51 radioactive atoms decayed.

Answer 1

A. number of decayed atoms = 73.197

Explanation:

In order to find the answer we need to use the radioactive decay equation:

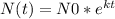`N(t)=N0*e^(kt)` where:

N0=initial radioactive atoms

t=time

k=radioactive decay constant

In our case, when t=0 we have 1,000,000 atoms, so:

`1,000,000=N0*e^(k*0)`

`1,000,000=N0`

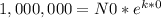
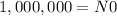
Now we need to find 'k'. Using the provied information that after 365 days we have 973,635 radioactive atoms, we have:

`973,635=1,000,000*e^(k*365)`

`ln(973,635/1,000,000)/365=k`

`-0.0000732=k`

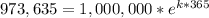
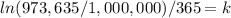
A. atoms decayed in a day:

`N(t)=1,000,000*e^(-0.0000732t)`

`N(1)=1,000,000*e^(-0.0000732*1)`

`N(1)= 999,926.803`

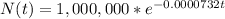
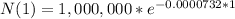
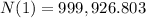
Number of atoms decayed in a day = 1,000,000 - 999,926.803 = 73.197

B. Because 'k' represents the probability of decay, then the probability that on a given day 51 radioactive atoms decayed is k=0.0000732.