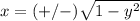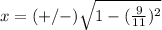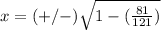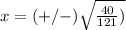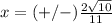Answer:
Part 1)
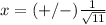 ----->
----->
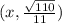
Part 2)
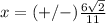 ---->
---->
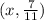
Part 3)
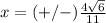 ---->
---->
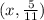
Part 4)
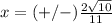 --->
--->
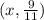
Explanation:
we know that
In the unit circle
The coordinates of a point have the following rule
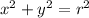
where
(x,y) are the coordinates of the point a r is the radius
but remember that in a unit circle the radius is equal to 1
so
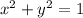
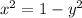
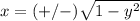
Find the x-coordinate of each case
Part 1) we have the point
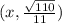
so
The y-coordinate is
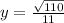
Find the value of the x-coordinate
substitute
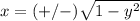
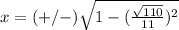
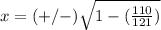
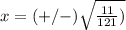
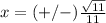
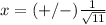
Part 2) we have the point
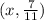
so
The y-coordinate is
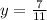
Find the value of the x-coordinate
substitute
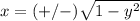
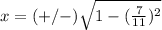
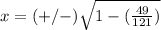
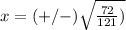
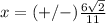
Part 3) we have the point
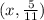
so
The y-coordinate is
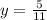
Find the value of the x-coordinate
substitute
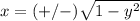
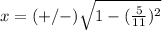
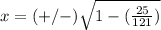
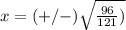
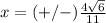
Part 4) we have the point
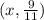
so
The y-coordinate is
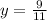
Find the value of the x-coordinate
substitute