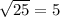Question

Identify the radius and center.

x^2 + y^2 + 4y -21 =0

Answer 1

radius 5

center (0,-2)

Explanation:

The goal is to get to
`(x-h)^2+(y-k)^2=r^2 \text{ where } (h,k) \text{ is the center and } r \text{ is the radius }`.

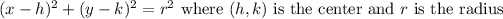We will need to complete the square for both parts.

That is we need to use:

`u^2+bu+((b)/(2))^2=(u+(b)/(2))^2`.

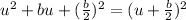First step is group the x's and y's together and put the constant on the opposing side. The x's and y's are already together. So we need to add 21 on both sides:

`x^2+y^2+4y=21`

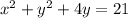
Now the x part is already done.

If you compare y^2+4y to
`u^2+bu+((b)/(2))^2=(u+(b)/(2))^2`

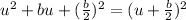
on the left side we have b is 4 so we need to add (4/2)^2 on both sides of
`x^2+y^2+4y=21`.

`x^2+y^2+4y+((4)/(2))^2=21+((4)/(2))^2`

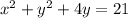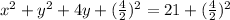
Now we can write the y part as something squared still using my completing the square formula:

`x^2+(y+(4)/(2))^2=21+2^2`

`x^2+(y+2)^2=21+4`

`(x-0)^2+(y+2)^2=25`

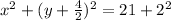
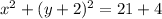
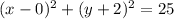
The center is (0,-2) and radius is
`√(25)=5`

Answer 2

Hello!

The answer is:

Center: (0,-2)

Radius: 2.5 units.

Why?

To solve the problem, using the given formula of a circle, we need to find its standard equation form which is equal to:

`(x-h)^(2)+(y-k)^(2)=r^(2)`

Where,

"h" and "k"are the coordinates of the center of the circle and "r" is its radius.

So, we need to complete the square for both variable "x" and "y".

The given equation is:

`x^2+y^2+4y-21=0`

So, solving we have:

`x^2+y^2+4y=21`

`x^2+(y^2+4y+((4)/(2))^(2))=21+((4)/(2))^(2)\\\\x^2+(y^2+4y+4)=21+4\\\\x^2+(y^2+2)=25`

`x^2+(y^2-(-2))=25`

Now, we have that:

`h=0\\k=-2\\r=√(25)=5`

So,

Center: (0,-2)

Radius: 5 units.

Have a nice day!

Note: I have attached a picture for better understanding.