Answer:
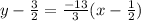 point-slope form
point-slope form
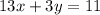 (standard form)
(standard form)
Let me know if you prefer another form.
Explanation:
The slope of a line can be found using
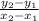 provided you are given two points on the line.
provided you are given two points on the line.
We are.
Now you can use that formula. But I really love to just line up the points vertically then subtract them vertically then put 2nd difference over 1st difference.
(4/5 , 1/5)
-( 1/2 , 3/2)
-----------------
3/10 -13/10
2nd/1st =
 is our slope.
is our slope.
So the following is point-slope form for a linear equaiton:
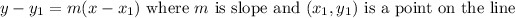
Plug in a point
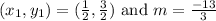 .
.
This gives:
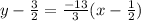
I'm going to distribute:
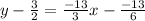
Now I don't like these fractions so I'm going to multiply both sides by the least common multiply of 2,3, and 6 which is 6:

Add 26x on both sides:

Add 9 on both sides:
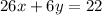 This is actually standard form of a line.
This is actually standard form of a line.
It can be simplified though.
Divide both sides by 2:
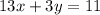 (standard form)
(standard form)