Answer:
second option
Explanation:
We are going to use the acronym:
"Soh Cah Toa".
Why? It tells us the right-triangle definitions of sine, cosine, and tangent.
sine is opposite over hypotenuse.
cosine is adjacent over hypotenuse.
tangent is opposite over adjacent.
So looking at our triangle with respect to B tells us that 3 is the opposite measurement and 6 is the adjacent. No matter what angle we are looking for in this triangle, the hypotenuse is constantly going to by
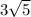 .
.
So let's look at cos(B).

We need to rationalize the denominator by multiplying top and bottom by sqrt(5):
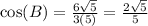
So now looking at sin(B).
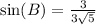
We have to rationalize again by multiplying top and bottom by sqrt(5):
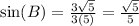 .
.
So looking at our triangle with respect to A tells us that 3 is the adjacent measurement and 6 is the opposite. No matter what angle we are looking for in this triangle, the hypotenuse is constantly going to by
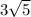 .
.
We don't have to use any trigonometric ratios with A.