Question

Through:(-2,5), perp. to y = 2x - 5

Answer 1

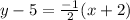`y-5=(-1)/(2)(x+2)` point-slope form

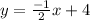`y=(-1)/(2)x+4` slope-intercept form

Explanation:

The slope-intercept form of a line is y=mx+b where m is the slope and b is the y-intercept.

The slopes of perpendicular lines are opposite reciprocals.

The slope of y=2x-5 is 2.

So we are looking for a line perpendicular to y=2x-5 which means we first to the take the opposite reciprocal of it's slope giving us:

opposite reciprocal of (2) is opposite (1/2)=-1/2.

So the slope of the line we are looking for is -1/2.

This means are equation for our line is in this form:

`y=(-1)/(2)x+b`

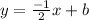
To find b we will use a point (x,y) that is on our line.

We are given a point (x,y)=(-2,5).

Plug this into our equation:

`5=(-1)/(2)(-2)+b`

`5=1+b`

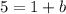
Subtract 1 on both sides:

`4=b`

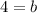
So the equation for our line that we are looking for is:

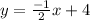`y=(-1)/(2)x+4` (slope-intercept form).

You could also go for point-slope form
`y-y_1=m(x-x_1)` where m is the slope and
`(x_1,y_1)` is a point on the line.

We have m=-1/2 and (x1,y1)=(-2,5) so our equation in point slope-form is:

`y-5=(-1)/(2)(x-(-2))`

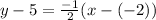
Simplifying just a hair:

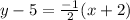`y-5=(-1)/(2)(x+2)`.