Answer:
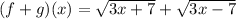
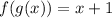
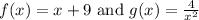

Let me know if you have any questions about any of my work.
Explanation:
You are given the following:

and asked to find
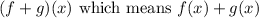 .
.
If you add those because we are asked to find f(x)+g(x) you get:
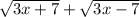
----------------------------------------------------------
You are given the following:
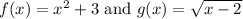
and asked to find
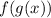 .
.
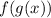
 I replaced g(x) with sqrt(x-2) because that is what it equals.
I replaced g(x) with sqrt(x-2) because that is what it equals.
Now this last thing means to replace old input in x^2+3 with new input sqrt(x-2) giving us:
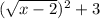
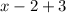
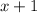
------------------------------------------------------------
We are given
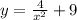 and asked to find g(x) and f(x) such that y=f(g(x)).
and asked to find g(x) and f(x) such that y=f(g(x)).
We have choices so let's use the choices:
Choice A:
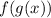
![f((4)/(x^2)){/tex] I replace g(x) with 4/x^2:</p><p>[tex](4)/(x^2)+9](https://img.qammunity.org/2020/formulas/mathematics/middle-school/5ou5vf1cgtp9jsn65dbrk289rbt14n1i28.png) I replaced the old input x with new input 4/x^2.
I replaced the old input x with new input 4/x^2.
This was actually the desired result.
-----------------------------------------------------------
To find the inverse of f(x)=3x-2 or y=3x-2, your objective is to swap x and y and then remake y the subject.
y=3x-2
Swap x and y:
x=3y-2
Now solve for y.
Add 2 on both sides:
x+2=3y
Divide both sides by 3:
(x+2)/3=y
y=(x+2)/3
