Answer:
1st problem:
Converges to 6
2nd problem:
Converges to 504
Explanation:
You are comparing to
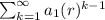
You want the ratio r to be between -1 and 1.
Both of these problem are so that means they both have a sum and the series converges to that sum.
The formula for computing a geometric series in our form is
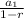 where
where
 is the first term.
is the first term.
The first term of your first series is 3 so your answer will be given by:
![(a_1)/(1-r)=(3)/(1-(1)/(2))=\frac{3}{(1)/(2)=6]()
The second series has r=1/6 and a_1=420 giving me:
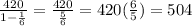 .
.