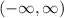Question

Solve the compound inequality 6b < 36 or 2b + 12 > 6.

Answer 1

All real numbers b ∈
`(-\infty, \infty)`

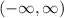
Explanation:

First we solve the following inequality

`6b < 36`

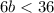
Divide by 6 both sides of the inequality

`b<(36)/(6)\\\\b<6`

The set of solutions is:

`(-\infty, 6)`

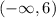
Now we solve the following inequality

`2b + 12 > 6`

Subtract 12 on both sides of the inequality

`2b + 12-12 > 6-12`

`2b> -6`

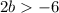
Divide by 2 on both sides of the inequality

`(2)/(2)b> -(6)/(2)`

`b> -3`

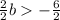
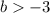
The set of solutions is:

`(-3, \infty)`

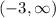
Finally, the set of solutions for composite inequality is:

`(-\infty, 6)` ∪
`(-3, \infty)`

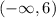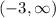
This is: All real numbers
`(-\infty, \infty)`

Answer 2

all values of b

Explanation:

6b < 36 or 2b + 12 > 6.

First solve the one on the left

6b < 36

Divide by 6

6b/6 < 36/6

b <6

Then solve the one on the right

2b + 12 > 6

Subtract 12 from each side

2b+12-12 >6-12

2b >-6

Divide by 2

2b/2 >-6/2

b >-3

b<6 or b >-3

Rewriting

b>-3 or b<6

b > -3 is an open circle at -3 with a line going to the right

b < 6 is an open circle at 6 with a line going to the left

The or means we add the lines together

We have a line going from negative infinity to infinity

all values of b