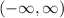Answer:
All real numbers b ∈
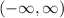
Explanation:
First we solve the following inequality
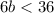
Divide by 6 both sides of the inequality
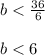
The set of solutions is:
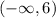
Now we solve the following inequality
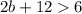
Subtract 12 on both sides of the inequality
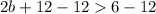
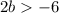
Divide by 2 on both sides of the inequality
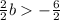
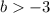
The set of solutions is:
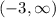
Finally, the set of solutions for composite inequality is:
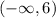 ∪
∪
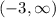
This is: All real numbers