Answer:
B.
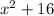
Explanation:
We are asked to find the prime polynomial from our given choices.
We know that a polynomial is prime, when it has only two factors that are 1 and polynomial itself.
Upon looking at our given choices, we can see that each polynomial can be factored except
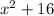 .
.
We can see that
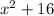 is sum of squares and sum of squares cannot be factored, therefore, polynomial
is sum of squares and sum of squares cannot be factored, therefore, polynomial
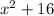 is a prime polynomial.
is a prime polynomial.