Question

The equation of a circle is given below. Identify the radius and center.

x^2 + y^2 - 6x -2y +1 = 0

Answer 1

The center is (3,1) and the radius is 3.

Explanation:

The goal is to write in
`(x-h)^2+(y-k)^2=r^2` because this tells us the center (h,k) and the radius r.

So we are going to need to complete the square 2 times here, once for x and the other time for y.

I'm going to use this formula to help me to complete the square:

`x^2+bx+((b)/(2))^2=(x+(b)/(2))^2`.

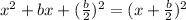So first step:

I'm going to group my x's together and my y's.

`x^2-6x+\text{ ___ }+y^2-2y+\text{ ___ }+1=0`

Second step:

I'm going to go ahead and subtract that one on both sides. Those blanks are there because I'm going to fill them in with a number so that I can write the x part and y part as a square. Remember whatever you add on one side you must add on the other. So I'm going to put 2 more blanks to fill in on the opposite side of the equation.

Third step:

Alright first blank I'm putting (-6/2)^2 due to my completing the square formula. That means this value will also go on the other side in on of those blanks.

In the second blank I'm going to put (-2/2)^2 due to the completing the square formula. This must also go on one of the blanks on the other side.

So we have:

`x^2-6x+((-6)/(2))^2+y^2-2y+((-2)/(2))^2=-1+((-6)/(2))^2+((-2)/(2))^2`

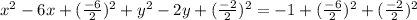
Fourth step:

Don't make this more hurtful than it already is. Just use the formula drag down the things inside the square. Remember this:

`x^2+bx+((b)/(2))^2`

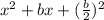
equals

`(x+(b)/(2))^2`.

We are applying that left hand side there (that bottom thing I just wrote).

Let's try it:

`(x+(-6)/(2))^2+(y+(-2)/(2))^2=-1+((-6)/(2))^2+((-2)/(2))^2`

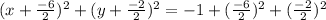
Fifth step:

The hard part is out of the way.

This is just a bunch of simplifying now:

`(x-3)^2+(y-1)^2=-1+9+1`

`(x-3)^2+(y-1)^2=9`

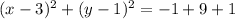
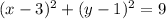
The center is (3,1) and the radius is 3.