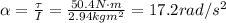(a)
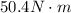
The torque exerted on the solid disk is given by
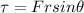
where
F is the magnitude of the force
r is the radius of the disk
 is the angle between F and r
is the angle between F and r
Here we have
F = 180 N
r = 0.280 m
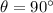 (because the force is applied tangentially to the disk)
(because the force is applied tangentially to the disk)
So the torque is
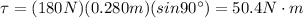
(b)
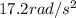
First of all, we need to calculate the moment of inertia of the disk, which is given by
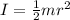
where
m = 75.0 kg is the mass of the disk
r = 0.280 m is the radius
Substituting,
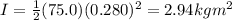
And the angular acceleration can be found by using the equivalent of Newtons' second law for rotational motions:
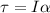
where
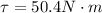 is the torque exerted
is the torque exerted
I is the moment of inertia
 is the angular acceleration
is the angular acceleration
Solving for
 , we find:
, we find: