Question

Find the distance from the point (8, 4) to the line y =
x+ 2.

Answer 1

The distance is
`3√(2)\ units`

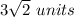
Explanation:

step 1

Find the slope of the give line

we have

y=x+2

so

the slope m is equal to

m=1

step 2

Find the slope of the perpendicular line to the given line

Remember that

If two lines are perpendicular, then their slopes are opposite reciprocal of each other

so

we have

m=1 -----> slope of the given line

therefore

The slope of the perpendicular line is equal to

m=-1

step 3

With m=-1 and the point (8,4) find the equation of the line

y-y1=m(x-x1)

substitute

y-4=-(x-8)

y=-x+8+4

y=-x+12

step 4

Find the intersection point lines y=x+2 and y=-x+12

y=x+2 -----> equation A

y=-x+12 ----> equation B

Adds equation A and equation B

y+y=2+12

2y=14

y=7

Find the value of x

y=x+2 -----> 7=x+2 -----> x=5

The intersection point is (5,7)

step 5

Find the distance between the point (8,4) and (5,7)

we know that

The distance from the point (8,4) to the line y=x+2 is equal to the distance from the point (8,4) to the point (5,7)

Find the distance AB

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

substitute

`d=\sqrt{(7-4)^(2)+(5-8)^(2)}`

`d=\sqrt{(3)^(2)+(-3)^(2)}`

`d=√(18)`

`d=3√(2)\ units`

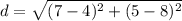
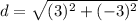
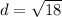
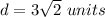
see the attached figure to better understand the problem