Question

Find the angle between the given vectors to the nearest tenth of a degree.

u = <6, -1>, v = <7, -4>

Answer 1

A

Explanation:

Given

u = <6, -1>

u = 6i-j

and

v=<7,-4>

v=7i-4j

The formula for angle is:

Let x be the angle

`cos\ x = (u.v)/(||u||.||v||)`

where ||u|| is the length and u.v is the dot product or scalar product of both vectors

So,

`||u|| = √((6)^2+(-1)^2)\\ = √(36+1)\\ = √(37)\\ ||v||=√((7)^2+(-4)^2)\\ = √(49+16)\\ = √(65)\\`

`u.v = u_1u_2+v_1v_2\\= (6)(7)+(-1)(-4)\\=42+4\\=46`

`cos\ x=(46)/(√(37)√(65)) \\= (46)/(√(2405) )\\Can\ also\ be\ written\ as:\\= (46)/(√(2405) ) * (√(2405) )/(√(2405)) \\=(46√(2405) )/(2405)`

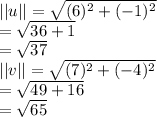
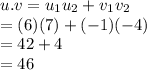
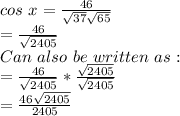
The calculated angle will be in radians. To find the angle in degrees:

`x = (180)/(\pi) cos^(-1) ((46√(2405) )/(2405))\\x = 20.282\\x= 20.3\\`

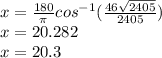
Hence Option A is correct ..