 is conservative if we can find a scalar function
is conservative if we can find a scalar function
 such that
such that
 . This would require
. This would require
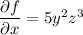
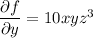
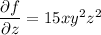
Integrate both sides of the first PDE with respect to
 :
:
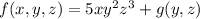 (*)
(*)
Differentiate both sides of (*) with respect to
 :
:
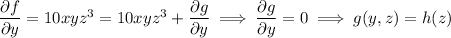
Differentiate both sides of (*) with respect to
 :
:

So we have
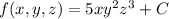
and so
 is indeed conservative.
is indeed conservative.