Question

Find the values for c and d

that would make the following
equation true,
(cy^2) (4y^d)=-20y^3

Answer 1

c=-5

d=1

Explanation:

`(cy^2)(4y^d)=-20y^3`

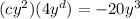
I'm going to reorder the left-hand side. Multiplication is commutative.

`(4c)(y^2y^d)=-20y^3`

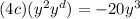
Since the bases are the same in
`y^2y^d` and the operation is multiplication, I'm going to add the exponents giving me:

`4cy^(2+d)=-20y^3`

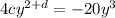
So this implies we have two equations to solve:

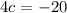`4c=-20` and
`2+d=3`

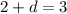
So the first equation can be solved by dividing both sides by 4 giving you
`c=-5`.

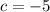The second equation can be solved by subtracting 2 on both sides giving you
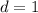`d=1`.