Question

Using a radar gun, you emit radar waves at a frequency of 6.2 GHz that bounce off of a moving tennis ball and recombine with the original waves. This produces a beat frequency of 969 Hz. How fast was the tennis ball moving?

Answer 1

23.4 m/s

Step-by-step explanation:

f = actual frequency of the wave = 6.2 x 10⁹ Hz

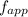`f_(app)` = frequency observed as the ball approach the radar

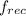`f_(rec)` = frequency observed as the ball recede away from the radar

V = speed of light

`v` = speed of ball

B = beat frequency = 969 Hz

frequency observed as the ball approach the radar is given as

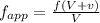`f_(app)=(f(V+v))/(V)` eq-1

frequency observed as the ball recede the radar is given as

`f_(rec)=(f(V-v))/(V)` eq-2

Beat frequency is given as

`B = f_(app) - f_(rec)`

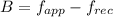
Using eq-2 and eq-1

`B = (f(V+v))/(V)- (f(V-v))/(V)`

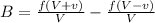
inserting the values

`969 = ((6.2* 10^(9))((3* 10^(8))+v))/((3* 10^(8)))- ((6.2* 10^(9))((3* 10^(8))-v))/((3* 10^(8)))`

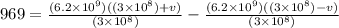
`v` = 23.4 m/s