Answer:
The magnitude of the angular momentum of the cylinder and the rotational kinetic energy of the cylinder are 0.0205 Kgm²/s and 0.01317 J
Step-by-step explanation:
Given that,
Moment of inertia = 0.016 kg m²
Radius = 6.0
Linear speed = 7.7 m/s
We need to calculate the angular momentum
Using formula of angular momentum

Where, L = angular momentum
I = moment of inertia
 =angular velocity
=angular velocity
Put the value into the formula
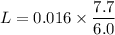
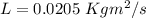
We need to calculate the rotational kinetic energy of the cylinder
Using formula of Rotational kinetic energy
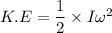
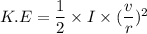
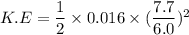
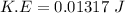
Hence, The magnitude of the angular momentum of the cylinder and the rotational kinetic energy of the cylinder are 0.0205 Kg m²/s and 0.01317 J