Question

The moment of inertia of a cylinder is 0.016 kg m^2 with radius 6.0 cm. (a) If the cylinder has a linear speed is 7.7 m/s, what is the magnitude of the angular momentum of the cylinder? (b) If the cylinder has a linear speed is 7.7 m/s, what is the magnitude of the rotational kinetic energy of the cylinder?

Answer 1

The magnitude of the angular momentum of the cylinder and the rotational kinetic energy of the cylinder are 0.0205 Kgm²/s and 0.01317 J

Step-by-step explanation:

Given that,

Moment of inertia = 0.016 kg m²

Radius = 6.0

Linear speed = 7.7 m/s

We need to calculate the angular momentum

Using formula of angular momentum

`L=I\omega`

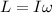
Where, L = angular momentum

I = moment of inertia

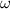`\omega` =angular velocity

Put the value into the formula

`L=0.016*(7.7)/(6.0)`

`L=0.0205\ Kg m^2/s`

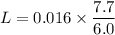
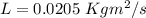
We need to calculate the rotational kinetic energy of the cylinder

Using formula of Rotational kinetic energy

`K.E=(1)/(2)* I\omega^2`

`K.E= (1)/(2)* I*((v)/(r))^2`

`K.E= (1)/(2)*0.016*((7.7)/(6.0))^2`

`K.E=0.01317\ J`

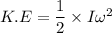
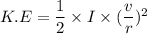
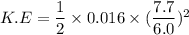
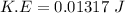
Hence, The magnitude of the angular momentum of the cylinder and the rotational kinetic energy of the cylinder are 0.0205 Kg m²/s and 0.01317 J