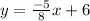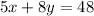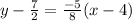Answer:
So our answers could be any of these depending on the form wanted*:
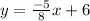
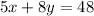

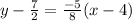
*There are other ways to write this equation.
Explanation:
So we are given two points on a line: (-8,11) and (4,7/2).
We can find the slope by using the formula
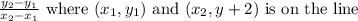 .
.
So to do this, I'm going to line up my points vertically and then subtract vertically, then put 2nd difference over 1st difference:
( 4 , 7/2)
-(-8 , 11)
----------------
12 -7.5
So the slope is -7.5/12 or -0.625 (If you type -7.5 division sign 12 in your calculator).
-0.625 as a fraction is -5/8 (just use the f<->d button to have your calculator convert your decimal to a fraction).
Anyways the equation of a line in slope-intercept form is y=mx+b where m is the slope and b is y-intercept.
We have m=-5/8 since that is the slope.
So plugging this into y=mx+b gives us y=(-5/8)x+b.
So now we need to find b. Pick one of the points given to you (just one).
Plug it into y=(-5/8)x+b and solve for b.
y=(-5/8)x +b with (-8,11)
11=(-5/8)(-8)+b
11=5+b
11-5=b
6=b
So the equation of the line in slope-intercept form is y=(-5/8)x+6.
We can also put in standard form which is ax+by=c where a,b,c are integers.
y=(-5/8)x+6
First step: We want to get rid of the fraction by multiplying both sides by 8:
8y=-5x+48
Second step: Add 5x on both sides:
5x+8y=48 (This is standard form.)
Now you can also out the line point-slope form,
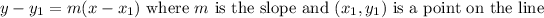
So you can say either is correct:
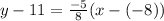
or after simplifying:

Someone might have decided to use the other point; that is fine:
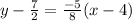
So our answers could be any of these depending on the form wanted*: