Question

Prove by induction that 3n(n 1) is divisible by 6 for all positive integers.

Answer 1

Answer with explanation:

We are asked to prove by the method of mathematical induction that:

3n(n+1) is divisible by 6 for all positive integers.

• for n=1 we have:

`3n(n+1)=3* 1(1+1)\\\\i.e.\\\\3n(n+1)=3* 2\\\\i.e.\\\\3n(n+1)=6`

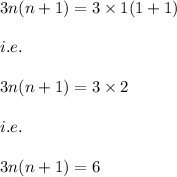
which is divisible by 6.

Hence, the result is true for n=1

• Let the result is true for n=k

i.e. 3k(k+1) is divisible by 6.

• Now we prove that the result is true for n=k+1

Let n=k+1

then

`3n(n+1)=3(k+1)* (k+1+1)\\\\i.e.\\\\3n(n+1)=3(k+1)(k+2)\\\\i.e.\\\\3n(n+1)=(3k+3)(k+2)\\\\i.e.\\\\3n(n+1)=3k(k+2)+3(k+2)\\\\i.e.\\\\3n(n+1)=3k^2+6k+3k+6\\\\i.e.\\\\3n(n+1)=3k^2+3k+6k+6\\\\i.e.\\\\3n(n+1)=3k(k+1)+6(k+1)`

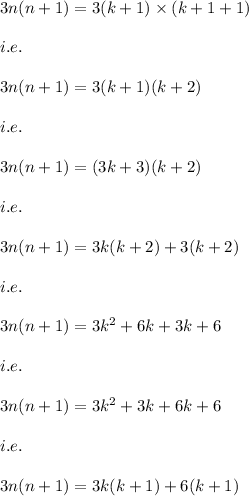
Since, the first term:

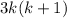`3k(k+1)` is divisible by 6.

( As the result is true for n=k)

and the second term
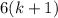`6(k+1)` is also divisible by 6.

Hence, the sum:

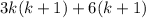`3k(k+1)+6(k+1)` is divisible by 6.

Hence, the result is true for n=k+1

Hence, we may say that the result is true for all n where n belongs to positive integers.