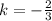Answer:
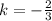
Explanation:
We are to find the constant of variation,
 , of the direct variation,
, of the direct variation,
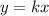 given the coordinates of the point
given the coordinates of the point
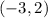 .
.
Direct variation is represented by:
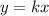
where
 is the constant of variation.
is the constant of variation.
Substituting the coordinates of the given point to find the value of
 .
.