Question

Oil with a density of 800 kg/m3 is pumped from a pressure of 0.6 bar to a pressure of 1.4 bar, and the outlet is 3 m above the inlet. The volumetric flow rate is 0.2 m3/s, and the inlet and exit areas are 0.06 m2 and 0.03 m3, respectively. (a) Assuming the temperature to remain constant and neglecting any heat transfer, determine the power input to the pump in kW. (b) What-if Scenario: What would the necessary power input be if the change in KE were neglected in the analysis??

Answer 1

23.3808 kW

20.7088 kW

Step-by-step explanation:

ρ = Density of oil = 800 kg/m³

P₁ = Initial Pressure = 0.6 bar

P₂ = Final Pressure = 1.4 bar

Q = Volumetric flow rate = 0.2 m³/s

A₁ = Area of inlet = 0.06 m²

A₂ = Area of outlet = 0.03 m²

Velocity through inlet = V₁ = Q/A₁ = 0.2/0.06 = 3.33 m/s

Velocity through outlet = V₂ = Q/A₂ = 0.2/0.03 = 6.67 m/s

Height between inlet and outlet = z₂ - z₁ = 3m

Temperature to remains constant and neglecting any heat transfer we use Bernoulli's equation

`\frac {P_1}{\rho g}+(V_1^2)/(2g)+z_1+h=\frac {P_2}{\rho g}+(V_2^2)/(2g)+z_2\\\Rightarrow h=(P_2-P_1)/(\rho g)+(V_2^2-V_1^2)/(2g)+z_2-z_1\\\Rightarrow h=((1.4-0.6)* 10^5)/(800* 9.81)+(6.67_2^2-3.33^2)/(2* 9.81)+3\\\Rightarrow h=14.896\ m`

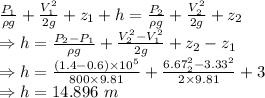
Work done by pump

`W_(p)=\rho gQh\\\Rightarrow W_(p)=800* 9.81* 0.2* 14.896\\\Rightarrow W_(p)=23380.8\ W`

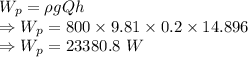
∴ Power input to the pump 23.3808 kW

Now neglecting kinetic energy

`h=(P_2-P_1)/(\rho g)+z_2-z_1\\\Righarrow h=((1.4-0.6)* 10^5)/(800* 9.81)+3\\\Righarrow h=13.19\ m\\`

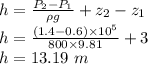
Work done by pump

`W_(p)=\rho gQh\\\Rightarrow W_(p)=800* 9.81* 0.2* 13.193\\\Rightarrow W_(p)=20708.8\ W`

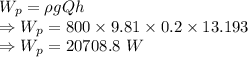
∴ Power input to the pump 20.7088 kW