Answer:
23.3808 kW
20.7088 kW
Step-by-step explanation:
ρ = Density of oil = 800 kg/m³
P₁ = Initial Pressure = 0.6 bar
P₂ = Final Pressure = 1.4 bar
Q = Volumetric flow rate = 0.2 m³/s
A₁ = Area of inlet = 0.06 m²
A₂ = Area of outlet = 0.03 m²
Velocity through inlet = V₁ = Q/A₁ = 0.2/0.06 = 3.33 m/s
Velocity through outlet = V₂ = Q/A₂ = 0.2/0.03 = 6.67 m/s
Height between inlet and outlet = z₂ - z₁ = 3m
Temperature to remains constant and neglecting any heat transfer we use Bernoulli's equation
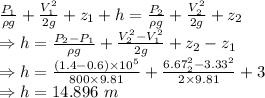
Work done by pump
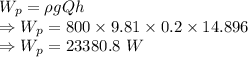
∴ Power input to the pump 23.3808 kW
Now neglecting kinetic energy
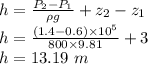
Work done by pump
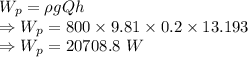
∴ Power input to the pump 20.7088 kW