Answer:
The area of the pattern is 43.6 inches²
Explanation:
* Lets explain how to solve the problem
- A decorative pillow can be modeled by Δ ABC
- In Δ ABC: AB = 9 inches , BC = 15 inches , AC = 10 inches
- To find the area of the triangle we can use the rule:
A = 1/2 × (AB) × (BC) × sin∠B
- We will use the cosine rule to find the measure of angle B
∵
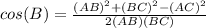
∵ AB = 9 , BC = 15 , AC = 10
∴
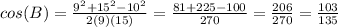
∴ m∠B =
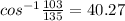 °
°
* Lets find the area of the triangle
∴ The area = 1/2 × (9) × (15) × sin(40.27) = 43.6 inches²
* The area of the pattern is 43.6 inches²