Question

Determine whether T : R^2 -->R^2,T((x.y)) = (x,y^2) is a linear transformation

Answer 1

Answer: No, the given transformation T is NOT a linear transformation.

Step-by-step explanation: We are given to determine whether the following transformation T : R² --> R² is a linear transformation or not :

`T(x,y)=(x,y^2).`

We know that

a transformation T from a vector space U to vector space V is a linear transformation if for
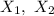`X_1,~X_2` ∈U and a, b ∈ R

`T(aX_1+bX_2)=aT(X_1)+bT(X_2).`

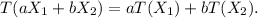
So, for (x, y), (x', y') ∈ R², and a, b ∈ R, we have

`T(a(x,y)+b(x',y'))\\\\=T(ax+bx',ay+by')\\\\=(ax+bx',(ay+by')^2)\\\\=(ax+bx',a^2y^2+2abyy'+y'^2)`

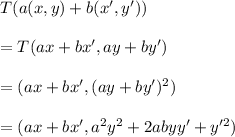
and

`aT(x,y)+bT(x',y')\\\\=a(x,y)+b(x', y'^2)\\\\=(ax+bx',ay+by')\\\\\\eq (ax+bx',a^2y^2+2abyy'+y'^2).`

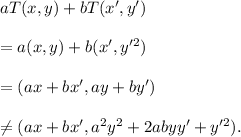
Therefore, we get

`T(a(x,y)+b(x',y'))\\eq aT(x,y)+bT(x',y').`

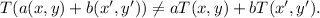
Thus, the given transformation T is NOT a linear transformation.