Question

Find the center of a circle with the equation: x2+y2−18x−14y+124=0

Answer 1

(9,7)

Explanation:

The goal is to write in standard form for a circle.

That is write in this form:
`(x-h)^2+(y-k)^2=r^2` where
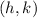`(h,k)` is the center and
`r` is the radius.

So you have

`x^2+y^2-18x-14y+124=0`

Reorder so you have your x's together, your y's together, and the constant on the other side:

`x^2-18x+y^2-14y=-124`

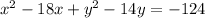
Now we are going to complete the square using

`x^2+bx+((b)/(2))^2=(x+(b)/(2))^2`.

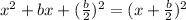This means we are going to add something in next to the x's and something in next to y's. Keep in mind whatever you add on one side you must add to the other.

`x^2-18x+((-18)/(2))^2+y^2-14y+((-14)/(2))^2=-124+((-18)/(2))^2+((-14)/(2))^2`

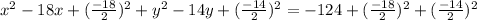
The whole reason we did is so we can write x^2-18x+(-9)^2 as (x-9)^2 and y^2-14y+(-7)^2 as (y-7)^2. We are just using this lovely thing I have I already mentioned:
`x^2+bx+((b)/(2))^2=(x+(b)/(2))^2`.

`(x-9)^2+(y-7)^2=-124+81+49`

`(x-9)^2+(y-7)^2=6`

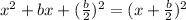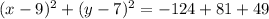
Comparing this to
`(x-h)^2+(y-k)^2=r^2` tells us

`h=9,k=7,r^2=6`

So the center is (9,7) while the radius is
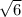`√(6)`.

Answer 2

Answer: (9,7)

Explanation:

The equation of the circle in Center-radius form is:

`(x - h)^2 + (y - k)^2 = r^2`

Where the center is at the point (h, k) and the radius is "r".

To rewrite the given equation in Center-radius form, we need to complete the square:

1. Move 124 to the other side of the equation:

`x^2+y^2-18x-14y+124=0\\\\x^2+y^2-18x-14y=-124`

2. Group terms:

`(x^2-18x)+(y^2-14y)=-124`

3. Add
`((-18)/(2))^2=81` to the group of the variable "x" and to the right side of the equation.

4. Add
`((-14)/(2))^2=49` to the group of the variable "y" and to the right side of the equation.

Then:

`(x^2-18x+81)+(y^2-14y+49)=-124+81+49`

5. Finally, simplify and convert the left side to squared form:

`(x-9)^2+(y-7)^2=6`

You can identify that the center of the circle is at:

`(h,k)=(9,7)`