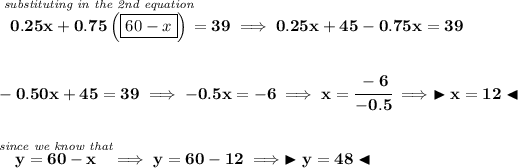Question

A metalworker has a metal alloy that is 25% copper and another alloy that is 75% copper. How many kilograms of each alloy should the metal worker combine to create 60kg of 65% copper alloy?

The metal worker should use _____ kilograms of the metal alloy that is 25% copper and _____ kilograms of the metal alloy that is 75% copper.

Answer 1

x=48

Explanation:

Answer 2

x = amount of the first alloy

y = amount of the second alloy

we know the first alloy is 25% copper, so then there is (25/100) * x of copper in it, namely 0.25x.

likewise, we know the second alloy is 75% copper so then there is (75/100) * y of copper or 0.75y.

he needs a 60 kgs mixture that 65% copper, or (65/100) * 60 = 39.

`\bf \begin{array}{lcccl} &\stackrel{kgs}{quantity}&\stackrel{\textit{\% of }}{copper}&\stackrel{\textit{kgs of }}{copper}\\ \cline{2-4}&\\ \textit{first Alloy}&x&0.25&0.25x\\ \textit{second Alloy}&y&0.75&0.75y\\ \cline{2-4}&\\ mixture&60&0.65&39 \end{array}~\hfill \begin{cases} x+y=60\\ \boxed{y}=60-x\\ \cline{1-1} 0.25x+0.75y=39 \end{cases}`

`\bf \stackrel{\textit{substituting in the 2nd equation}}{0.25x+0.75\left( \boxed{60-x} \right)}=39\implies 0.25x+45-0.75x=39 \\\\\\ -0.50x+45=39\implies -0.5x=-6\implies x=\cfrac{-6}{-0.5}\implies \blacktriangleright x = 12 \blacktriangleleft \\\\\\ \stackrel{\textit{since we know that}}{y=60-x}\implies y=60-12\implies \blacktriangleright y=48 \blacktriangleleft`