Answer:
Answer is part d -736.88 psi
Step-by-step explanation:
We know that for a bar subjected to pure torsion the shear stresses that are generated can be calculated using the following equation
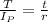 ....................(i)
....................(i)
Where
T is applied Torque
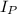 is the polar moment of inertia of the shaft
is the polar moment of inertia of the shaft
t is the shear stress at a distance 'r' from the center
r is the radial distance
Now in our case it is given in the question T =82.7 ft*lbs
converting T into inch*lbs we have T = 82.7 x 12 inch*lbs =992.4 inch*lbs
We also know that for a circular shaft polar moment of inertia is given by
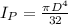
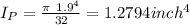
Since we are asked the maximum value of shearing stresses they occur at the surface thus r = D/2
Applying all these values in equation i we get
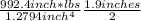 = t
= t
Thus t = 736.88 psi