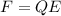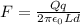Question

A point charge Q is located a distance d away from the center of a very long charged wire. The wire has length L >> d and total charge q. What force does the wire experience?

Answer 1

`F = (Qq)/(2\pi \epsilon_0 L d)`

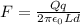
Step-by-step explanation:

As we know that if a charge q is distributed uniformly on the line then its linear charge density is given by

`\lambda = (q)/(L)`

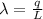
now the electric field due to long line charge at a distance d from it is given as

`E = (2k\lambda)/(d)`

`E = (q)/(2\pi \epsilon_0 d)`

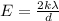
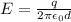
now the force on the other charge in this electric field is given as

`F = QE`

`F = (Qq)/(2\pi \epsilon_0 L d)`