Answer:-0.4199 J/k
Step-by-step explanation:
Given data
mass of nitrogen(m)=1.329 Kg
Initial pressure
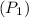 =120KPa
=120KPa
Initial temperature
 300k
300k
Final volume is half of initial
R=particular gas constant
Therefore initial volume of gas is given by
PV=mRT
V=0.986\times 10^{-3}
Using
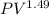 =constant
=constant
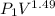 =
=
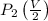
 =337.066KPa
=337.066KPa
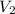 =
=

and entropy is given by
 =
=
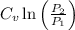 +
+
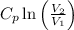
Where,
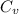 =
=
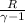 =0.6059
=0.6059
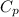 =
=
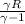 =0.9027
=0.9027
Substituting values we get
 =
=
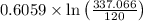 +
+

 =-0.4199 J/k
=-0.4199 J/k