Rolle's theorem works for a function
 over an interval
over an interval
![[a,b]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x9eybysx3cihgn4xxsxk4fl3z5dcnyp7ww.png) if:
if:
 is continuous on
is continuous on
![[a,b]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x9eybysx3cihgn4xxsxk4fl3z5dcnyp7ww.png)
 is differentiable on
is differentiable on
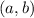
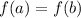
This is our case:
 is a polynomial, so it is continuous and differentiable everywhere, and thus in particular it is continuous and differentiable over [0,4].
is a polynomial, so it is continuous and differentiable everywhere, and thus in particular it is continuous and differentiable over [0,4].
Also, we have
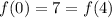
So, we're guaranteed that there exists at least one point
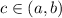 such that
such that
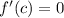 .
.
Let's compute the derivative:

And we have
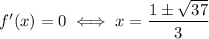
In particular, we have

so this is the point that satisfies Rolle's theorem.