Answer:
T = 1.17 x
 N-m
N-m
Step-by-step explanation:
Given :
Gap between the two plates , dy = 1 mm
dy = 1 x
 m
m
Angular velocity of the top plate , ω = 5 rad/s
Diameter of the plate, D = 20 cm
Radius of the plate, R = 10 cm
= 0.1 m
Temperature of the kerosene = 40°C
Viscosity of kerosene at 40°C = 0.0015 Pa-s
Now let us take a small elemental ring of thickness dr at a radius r.
Therefore, area of this elemental ring of dr = 2πrdr
Now linear velocity at radius r = ω x r
5r m/s
Now applying Newtons law of viscosity we get,
Shear stress, τ = μ.
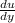
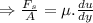
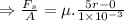
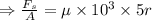
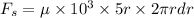

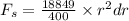
Now we know torque due to small strip,
dT =
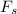 x r
x r
dT =
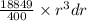
Therefore total torque for r=0 to r=R can be calculated. So by integrating,



T = 1.17 x
 N-m
N-m