Answer: 95.45 %
Explanation:
Given : The distribution is bell shaped , then the distribution must be normal distribution.
Mean :
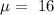
Standard deviation :
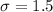
The formula to calculate the z-score :-

For x = 13
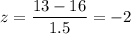
For x = 19
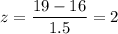
The p-value =
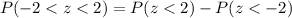
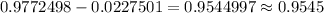
In percent,
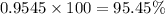
Hence, the percentage of data lie between 13 and 19 = 95.45 %