Answer:
1. The slope of the line is
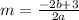 .
.
2. The value of a is 18.
Explanation:
If a line passes through two points, then the slope of the line is

(1)
It is given that the line passes through the points (-a + 3, b - 3) and (a + 3, -b). So, the slope of the line is
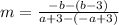
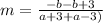
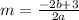
The slope of the line is
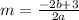 .
.
(2)
If the line passing through the points (a, 1) and (6, 5), then the slope of the line is
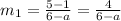
If the line passing through the points (2, 7) and (a + 2, 1), then the slope of the line is
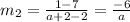
The slopes of two parallel lines are same.
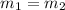
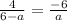
On cross multiplication we get
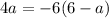

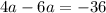
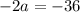
Divide both sides by -2.
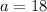
Therefore the value of a is 18.