Question

Suppose you invest $5,000 per year, for 10 years, into an account with an annual rate of return of 7%. Deposits are made at the end of each year. Starting in the next year (Year 11), what is the maximum amount you can withdraw each year for the next 17 years, assuming the rate of return is now 6% per year?

Answer 1

Step-by-step explanation:

The timeline would be as follows:

During the first 10 years, we deposit 5,000 at 7% market rate.

Then we withdraw at the beginning of Year eleven during 17 year. The market price for this period is 6%

First Step amount at end of year 10

`C * ((1+r)^(time) - 1 )/(rate) = FV\\`

`5,000 * ((1+0.07)^(10) - 1 )/(0.07) = FV\\`

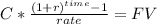
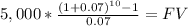
FV = $69,082.24

Then, we are going to calculate how much can be withdraw during 17 years

At the beginning of the period at 6% rate

`C = PV (rate)/(1-(1+rate)^(-time) )/ (1+rate)`

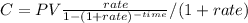
From the PV formula, we clear the Cuota and then we divide by 1.06 because we are doing an annuity-due. The amount is withdraw at the beginning of the period. That's why we add a new element.

`C = 69,082.24 (0.06)/(1-(1.06)^(-17) ) /(1.06)`

C = 6220.32