Question

You just purchased two coins at a price of $670 each. Because one of the coins is more collectible, you believe that its value will increase at a rate of 7.1 percent per year, while you believe the second coin will only increase at 6.5 percent per year. If you are correct, how much more will the first coin be worth in 15 years?

Answer 1

The value of first coin will be $151.51 more than second coin in 15 years.

Explanation:

You have just purchased two coins at a price of $670 each.

You believe that first coin's value will increase at a rate of 7.1% and second coin's value 6.5% per year.

We have to calculate the first coin's value after 15 years by using the formula

`A=P(1+(r)/(100))^(n)`

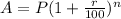
Where A = Future value

P = Present value

r = rate of interest

n = time in years

Now we put the values

`A=670(1+(7.1)/(100))^(15)`

`A=670(1+0.071)^(15)`

`A=670(1.071)^(15)`

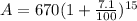
A = (670)(2.797964)

A = 1874.635622 ≈ $1874.64

Now we will calculate the value of second coin.

`A=670(1+(6.5)/(100))^(15)`

`A=670(1+0.6.5)^(15)`

`A=670(1.065)^(15)`

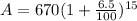
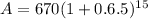
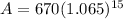
A = 670 × 2.571841

A = $1723.13

The difference of the value after 15 years = 1874.64 - 1723.13 = $151.51

The value of first coin will be $151.51 more than second coin in 15 years.