Question

The Chesapeake Bay tides vary between 4 feet and 6 feet. The tide is at its lowest point when time (t) is 0 and completes a full cycle in 12 hours. What is the amplitude, period, and midline of a function that would model this periodic phenomenon?

Amplitude = 1 foot; period = 12 hours; midline: y = 5

Amplitude = 2 feet; period = 6 hours; midline: y = 1

Amplitude = 2 feet; period = 12 hours; midline: y = 5

Answer 1

Amplitude = 1 foot; period = 12 hours; midline: y = 5

Explanation:

The Chesapeake Bay tides vary between 4 feet and 6 feet.

This means the range is

`4 \leqslant f(t) \leqslant 6`

The period is the length of the interval on which the function completes one full cycle.The tide is at its lowest point when time (t) is 0 and completes a full cycle in 12 hours.

The interval is [0,12] and its length is 12, hence the period is 12.

The midline

`y = (min + max)/(2)`

`y = (4 + 6)/(2) = 5`

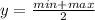
The amplitude is the distance from the midline to the peak.

The amplitude is |5-4|=|5-6|=1

The first choice is correct.