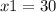Answer:
The value of the greater number is 30.
Explanation:
We need to find the values of x that satisfy the equation :
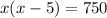
Working with the equation ⇒
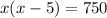
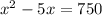
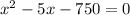
Given an equation with the form
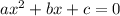
We can use the quadratic equation to find the values of x
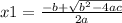 and
and

With
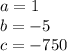 we replace in the equations of x1 and x2 ⇒
we replace in the equations of x1 and x2 ⇒
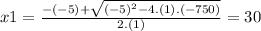
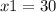 is a solution of the equation
is a solution of the equation
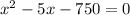
Now for x2 ⇒
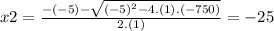
 is a solution of the equation
is a solution of the equation
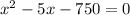
Given that both numbers are positive ⇒
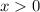 and
and
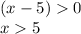
Therefore, x2 is not a possible value for the greater number
The greater number is