Question

Complete the square for the following quadratic equation to determine its solutions and the location of its extreme value

y = -x + 4x + 12
A
x=2 + 277
extreme value at (2.16)
B.
X = -2,6
extreme value at (2,12)
C.
x = -2.6
extreme value at (2.16)
D. X = 2 + 277
extreme value at (2,12)

Answer 1

Option C. x = -2,6 extreme value at (2.16)

Explanation:

we have

`y=-x^2+4x+12`

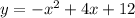
This is the equation of a vertical parabola open down

The vertex is a maximum (extreme value)

Convert the equation into vertex form

`y=-x^2+4x+12`

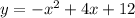
Complete the square

Group terms that contain the same variable and move the constant term to the left side

`y-12=-x^2+4x`

Factor -1

`y-12=-(x^2-4x)`

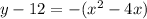
Remember to balance the equation by adding the same constants to each side.

`y-12-4=-(x^2-4x+4)`

Rewrite as perfect squares

`y-16=-(x-2)^2`

`y=-(x-2)^2+16` -----> equation of the parabola in vertex form

The vertex is the point (2,16) ----> is a maximum (extreme value)

Determine the solutions of the quadratic equation

For y=0

`0=-(x-2)^2+16`

`(x-2)^2=16`

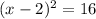
square root both sides

`(x-2)=(+/-)4`

`x=2(+/-)4`

`x=2(+)4=6`

`x=2(-)4=-2`

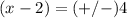
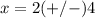
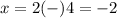
therefore

The solutions are x=-2 and x=6

The extreme value is (2,16)