Question

If x= 6 is the only x-intercept of the graph of a quadratic equation, which statement best describes the discriminant of the

equation?

Answer 1

discriminant is zero (0)

Explanation:

Actually, you have a double root here: {6, 6}: "two real, equal roots." That tells us immediately that the value of the discriminant was zero (0).

Answer 2

The discriminant of the equation is zero.

Explanation:

The given graph is a quadratic equation. If x = 6 is the only x-intercept of the graph, then the roots must be equal.

The quadratic equation will have two solutions. Here the two solutions are equal x = 6.

If the roots are equal, then the discriminant is zero.

The factors of the quadratic equation (x - 6) (x - 6)

=
`x^2 - 6x - 6x + 36`

=
`x^2 -12x + 36`

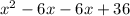
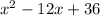
Discriminant =
`b^2 - 4ac`

Here a = 1, b = -12 and c = 36

Discriminant =
`(-12)^(2) - 4.1.36`

= 144 - 144

= 0

Therefore, the answer is "The discriminant of the equation is zero."