Answer:
The length of segment XY can be found by solving for a in
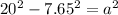
The measure of the central angle
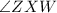 is
is
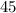 .
.
Explanation:
If the regular octagon has a perimeter of 122.4cm, then each side is
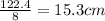
The measure of each central angle is
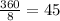
The angle between the apothem and the radius is
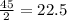
The segment XY=a is the height of the right isosceles triangle.
We can use the Pythagoras Theorem with right triangle XYZ to get:
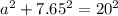
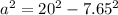
Therefore, the correct options are:
The length of segment XY can be found by solving for a in
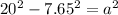
The measure of the central angle
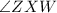 is
is
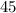 .
.