Answer:
So length is 7 in while width is 1 in.
Explanation:
We are given W is 6 inches less than L which mean as an equation we have W=L-6.
We are given the area of this rectangle, LW=7.
So we have the system:
W=L-6
LW=7.
Replace the second W with what the first W equals:
LW=7
L(L-6)=7
Distribute:
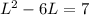
Subtract 7 on both sides:
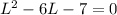
We are luck since the coefficient of L^2 is 1. This means all we have to do is find two numbers that multiply to be -7 add at the same time add up to -6.
Those numbers are -7 and 1 since (-7)(1)=-7 and (-7)+(1)=-6.
So the factored form of our equation is:
(L-7)(L+1)=0
This gives us two equations to solve:
L-7=0 or L+1=0
L=7 or L=-1
L=-1 doesn't make sense for a length so L=7.
L=7 means the length is 7 inches.
If W=L-6 and L=7, then W=7-6=1.
The width is 1 inch since W=1.
So length is 7 in while width is 1 in.