Question

Water is flowing at a rate of 0.15 ft3/s in a 6 inch diameter pipe. The water then goes through a sudden contraction to a 2 inch diameter pipe. What is the head loss through this contraction

Answer 1

Head loss=0.00366 ft

Step-by-step explanation:

Given :Water flow rate Q=0.15
`(ft^(3))/(sec)`

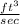
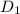`D_(1)`= 6 inch=0.5 ft

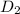`D_(2)`=2 inch=0.1667 ft

As we know that Q=AV

`A_(1)* V_(1)=A_(2)* V_(2)`

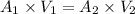
So
`V_(2)=(Q)/(A_2)`

`V_(2)=(.015)/((3.14)/(4)* 0.1667^(2))`

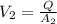
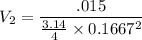
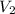`V_{2`=0.687 ft/sec

We know that Head loss due to sudden contraction

`h_(l)=K(V_(2)^2)/(2g)`

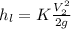
If nothing is given then take K=0.5

So head loss
`h_(l)=(0.5)\frac{{0.687}^2}{2* 32.18}`

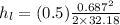
=0.00366 ft

So head loss=0.00366 ft