Question

Find the dimensions of a circular cross section steel bar subjected to tension by a force N 20000 N in two hypotheses: a) the maximum allowable stress is 150 N/mm2, b) the maximum acceptable strain is 0.0005. Take E 207GPa

Answer 1

a). d = 13 mm

b). d = 16 mm

Step-by-step explanation:

a). Given :

Force = 20000 N

Maximum stress, σ = 150 N/
`mm^(2)`

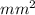
Therefore, we know that that

σ =
`(Force)/(area)`

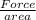
150 = \frac{Force}{\frac{pi}{4}\times d^{2}}

150 = \frac{20000}{\frac{pi}{4}\times d^{2}}

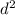`d^(2)` = 169.76

d = 13.02 mm

d
`\simeq` 13 mm

b). Given :

Strain, ε = 0.0005

Young Modulus, E = 207 GPa

= 207
`*`
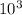`10^(3)` MPa

Therefore we know that, Stress σ = E
`*`ε

= 207
`*`
`10^(3)`
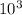
`*`0.0005

= 103.5 N/
`mm^(2)`

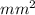
We know that

σ =
`(Force)/(Area)`

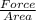
103.5 =
`(Force)/((pi)/(4)* d^(2))`

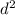`d^(2)` = 246.27

d = 15.69 mm

d
`\simeq`16 mm

Answer 2

d = 13 mm

d = 15.68 mm

Step-by-step explanation:

Given data

force = 20000 N

stress = 150 N/mm²

strain = 0.0005

E = 207 GPa

Solution

we know stress = force / area

so 0.0005 = 20000 / area

area =
`\pi`/4 × d²

put the area in stress equation and find out d

d² = 4×force /
`\pi` ×stress

d² = 4× 20000 /
`\pi` ×150

d =
`\sqrt{ 4× 20000 / [tex]\pi` ×150}[/tex]

d = 13 mm

and now we know starin = stress / E

same like stress we find d here

d =
`\sqrt{ 4× 20000 / [tex]\pi` ×0.0005×207×10³ }[/tex]

so d = 15.68 mm