Answer:
a). d = 13 mm
b). d = 16 mm
Step-by-step explanation:
a). Given :
Force = 20000 N
Maximum stress, σ = 150 N/
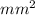
Therefore, we know that that
σ =
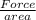
150 = \frac{Force}{\frac{pi}{4}\times d^{2}}
150 = \frac{20000}{\frac{pi}{4}\times d^{2}}
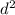 = 169.76
= 169.76
d = 13.02 mm
d
 13 mm
13 mm
b). Given :
Strain, ε = 0.0005
Young Modulus, E = 207 GPa
= 207

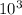 MPa
MPa
Therefore we know that, Stress σ = E
 ε
ε
= 207

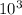
 0.0005
0.0005
= 103.5 N/
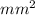
We know that
σ =
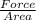
103.5 =
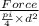
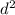 = 246.27
= 246.27
d = 15.69 mm
d
 16 mm
16 mm