Question

In a gas turbine, air (kinematic viscosity of 1x104-5 m 2/s) flows over a 2 cm long turbine blade at 100 m/s. How long should the blade be in my lab's wind tunnel (air, kinematic viscosity of 1.5x10A-5 mA2/s, velocity of 10 m/s), to match the Reynolds number of the gas turbine? a)-2cm b)-30cm c)-0.3cm

Answer 1

30 cm

Step-by-step explanation:

For Reynold's number similarity between model and prototype we should have

`R_(e)  _(model) =R_{_(e prototype)}  \\\\(V_(model) L_(model) )/(kinematic viscosity in model) =(V_(proto)L_(proto)  )/(kinematic viscosity in prototype)`

Given L(prototype)= 2cm

V(prototype) = 100m/s

V(model) = 10m/s

Thus applying values in the above equation we get

`\frac{100m/s^{} X2cm^{}  }{1X10^(-5)m^(2)/s  } =(L_(M)X10m/s )/(1.5X10^(-5)m^(2)/s )`

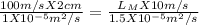
Solving for Lmodel we get Lm = 30cm