Question

Determine the constant speed at which the cable at A must be drawn in by the motor in order to hoist the load 6 m in 1.5s

Answer 1

4m/s

Step-by-step explanation:

We know that power supplied by the motor should be equal to the rate at which energy is increased of the mass that is to be hoisted

Mathematically

`Power_(motor) } =(Energy )/(time)`\

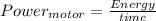We also know that Power = force x velocity ..................(i)

The force supplied by the motor should be equal to the weight (mg) of the block since we lift the against a force equal to weight of load

=> power = mg x Velocity........(ii)

While hoisting the load at at constant speed only the potential energy of the mass increases

Thus Potential energy = Mass x g x H...................(iii)

where

g = accleration due to gravity (9.81m/s2)

H = Height to which the load is hoisted

Equating equations (ii) and (iii) we get

m x g x v =
`(mgh)/(t)`

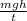
thus we get v = H/t

Applying values we get

v = 6/1.5 = 4m/s